![]()
![]()
|
|
|
|
|
|
Exercice |
|
|
|
|
|
Extraits de l'ouvrage de Newton "Les principes mathématiques de la philosophie naturelle", d'après la traduction de Mme de Chastelet (1756-1759).
Extraits du livre I :
Proposition I :
Les forces par lesquelles les satellites de Jupiter sont retirés
perpétuellement du mouvement rectiligne (...), sont dirigées vers le centre de
Jupiter et sont inversement proportionnelles aux carrés de leur distance à ce
centre.
Proposition V :
Les satellites de Jupiter gravitent vers Jupiter, ceux de Saturne vers
Saturne, et les planètes principales vers le Soleil, et c'est par la force de
leur gravité que ces corps (...) sont retirés à tout moment de la ligne droite
et qu'ils sont retenus dans des orbites curvilignes.
Proposition VI :
Tous les corps gravitent vers chaque planète et, sur la même planète, (...)
leurs forces de gravité, à égale distance du centre, sont proportionnelles à la
masse que chacun d'eux contient.
On considère que tous les satellites et planètes sont des corps dont la répartition de la masse est à symétrie sphérique. Les mouvements sont étudiés dans le référentiel "jupitérocentrique" (d'origine le centre de Jupiter et d'axes dirigés vers trois étoiles fixes). On note M la masse de Jupiter et G la constante de gravitation universelle.
1. On étudie le champ de gravitation de Jupiter.
1.1. Donner l'expression vectorielle de la force d'interaction
gravitationnelle exercée par Jupiter sur un de ses satellites de masse m et
situé à la distance r du centre O de Jupiter.
Faire un schéma explicatif.
1.2. Donner, dans les propositions ci-dessus extraites du livre I, les
citations en accord avec cette expression vectorielle.
1.3. Donner l'expression vectorielle du champ de gravitation
![]() créé par Jupiter, à la
distance r de son centre.
créé par Jupiter, à la
distance r de son centre.
1.4. Représenter quelques lignes du champ de gravitation autour de Jupiter.
1.5. Pourquoi est-il important de préciser que la répartition de la masse des
corps est à symétrie sphérique ?
2. On considère que Ganymède, un satellite de Jupiter, satellite de masse m, est soumis à la seule force de gravitation due à Jupiter et que son mouvement est circulaire de centre O (centre de Jupiter) et de rayon r.
2.1. Montrer que le mouvement du satellite est uniforme.
2.2. Etablir l'expression de la vitesse v de Ganymède en fonction de G, M et r ;
en déduire l'expression de la période T de révolution.
2.3. Parmi les plus gros satellites de Jupiter, Europe gravite à raison de 14 km
par seconde alors que Ganymède met 1 minute pour parcourir 660 km.
Quel est le satellite le plus éloigné de Jupiter ? Justifier.
3. On considère que Ganymède se déplace sur son orbite de A en C en 1 seconde (voir figure 1) et que le rayon r de cette orbite est de l'ordre de un million de kilomètres.
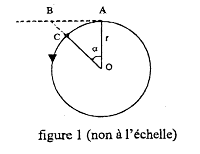
3.1. D'après les extraits cités, que représente la droite AB sur la figure 1 ?
3.2. Si ![]() (en radian) est
très petit, BC est égal à
(en radian) est
très petit, BC est égal à ![]() .
.
En déduire que BC est aussi égal à
![]() , où
arc (AC) représente l'arc de cercle entre A et C.
, où
arc (AC) représente l'arc de cercle entre A et C.
Vérifier que la distance BC vaut environ 6 cm.
3.3. Supposons qu'on laisse tomber une pierre de l'altitude de Ganymède en
direction de Jupiter. On admet que la hauteur de chute, pendant la première
seconde, se calcule par l'expression
![]() , G
représentant la valeur du champ de gravitation à cette altitude, soit G =
0,12 m.s-2.
, G
représentant la valeur du champ de gravitation à cette altitude, soit G =
0,12 m.s-2.
Calculer la hauteur de chute durant la première seconde.
3.4. Compte tenu des résultats des questions 3.2 et 3.3 et des propositions de
Newton, que représente BC pour Ganymède ?
1.1 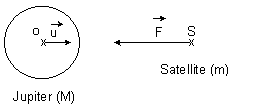
![]()
1.2 Les citations concernées sont :
1.3
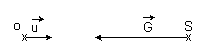
Le champ de gravitation créé par Jupiter en S est :
![]()
1.4 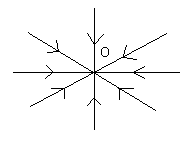
Les lignes de champ sont radiales, orientées vers le centre O de Jupiter.
1.5 Si la répartition de la masse des corps est à symétrie sphérique, on peut alors considérer que toute la masse du corps est concentrée en son centre : condition d'application de la formule de Newton appliquée au 1.1.
| 2.1 Référentiel : jupiterocentrique supposé galiléen |
| Système : Ganymède (satellite) |
| Bilan des
forces : |
| Théorème du
centre d'inertie : |
La force gravitationnelle
![]() est radiale
centripète ; or le satellite a un mouvement circulaire
est radiale
centripète ; or le satellite a un mouvement circulaire
![]()
![]() est normale
centripète.
est normale
centripète.
Donc, dans la base de Frenet :
![]()
On a : ![]() donc le mouvement
est uniforme.
donc le mouvement
est uniforme.
2.2 ![]() et
et
![]() donc
donc
![]() (3)
(3)
or ![]() d'où
d'où
![]()
2.3 En ![]() , Europe
parcourt
, Europe
parcourt ![]() alors que
Ganymède ne parcourt que
alors que
Ganymède ne parcourt que ![]() .
D'après (3) plus r est grand, plus v est petit, c'est donc Ganymède qui gravite
le plus loin des deux de Jupiter.
.
D'après (3) plus r est grand, plus v est petit, c'est donc Ganymède qui gravite
le plus loin des deux de Jupiter.
3.1 D'après les extraits cités, la droite AB représente la trajectoire de laquelle les satellites sont retirés à tout moment par la force de leur gravité.
3.2 Par définition
![]() d'où
d'où ![]() or
or
![]() donc
donc
![]() .
.
On a donc bien
![]() .
.
Pour Ganymède : ![]() donc
donc
![]() .
.
AN : ![]()
3.3 Cette hauteur de chute en
![]() est :
est :
![]()
AN : ![]() soit
soit
![]() .
.
3.4 Comme on trouve
![]() ,
on peut dire que BC représente la hauteur de chute de Ganymède en 1 seconde.
,
on peut dire que BC représente la hauteur de chute de Ganymède en 1 seconde.